Intro

在深度学习领域，卷积神经网络（CNNs）已经成为了图像处理和计算机视觉任务中最重要的技术之一。卷积操作是 CNNs 中最基础的操作之一，它可以有效地提取出图像中的特征，并使用这些特征来识别物体，主要应用于图像处理、语音识别、自然语言处理等领域。

然而，有时候我们需要将图像进行上采样，也就是将其放大或扩展到更大的尺寸。为了实现这个目的，我们需要使用一种叫做 ConvTranspose2d 的操作，它也被称为转置卷积。

在本文中，我们将深入研究卷积和转置卷积的原理、应用和代码实现。我们将讨论卷积和转置卷积的数学原理，包括矩阵乘法和张量的形状等。我们还将探讨卷积和转置卷积的一些应用，例如转置卷积在生成对抗网络（GANs）中的图像生成和图像分割任务中的应用。最后，我们还将提供 Python 代码实现，以演示它们的工作原理。

数学原理

卷积

Convolution

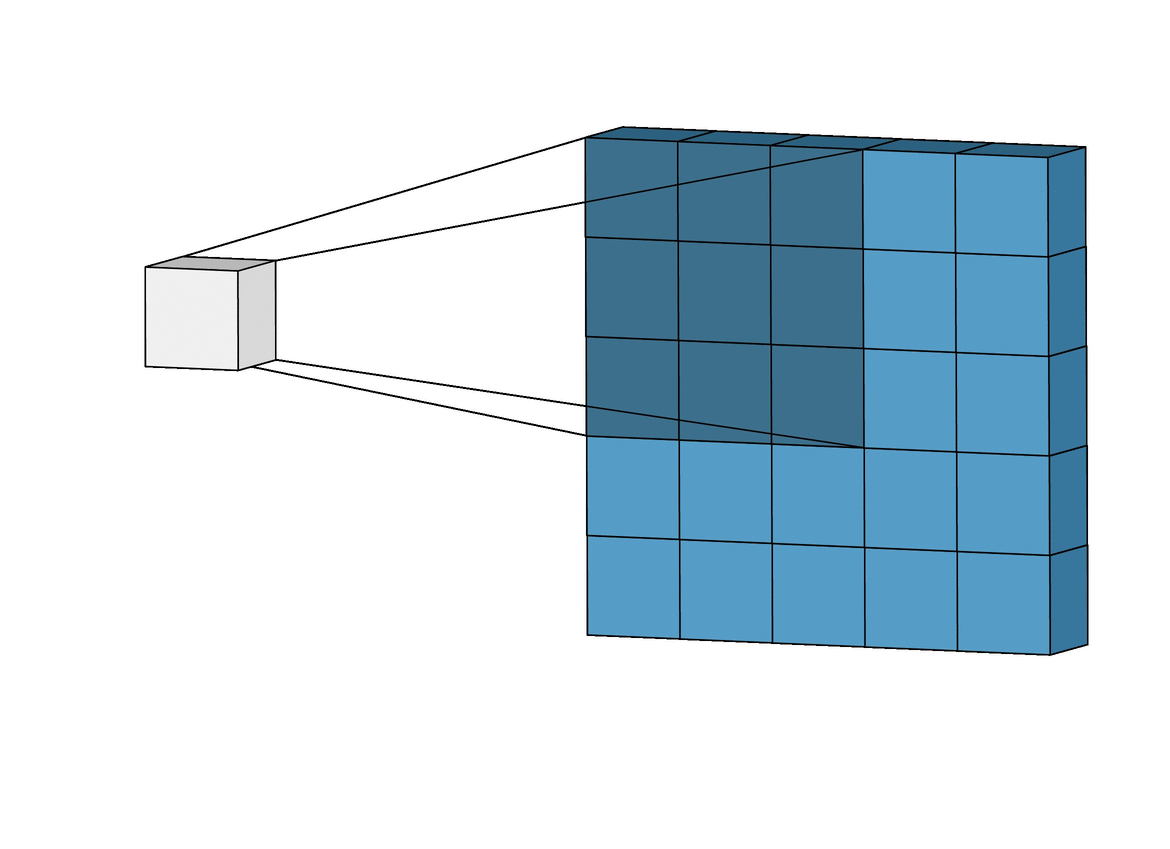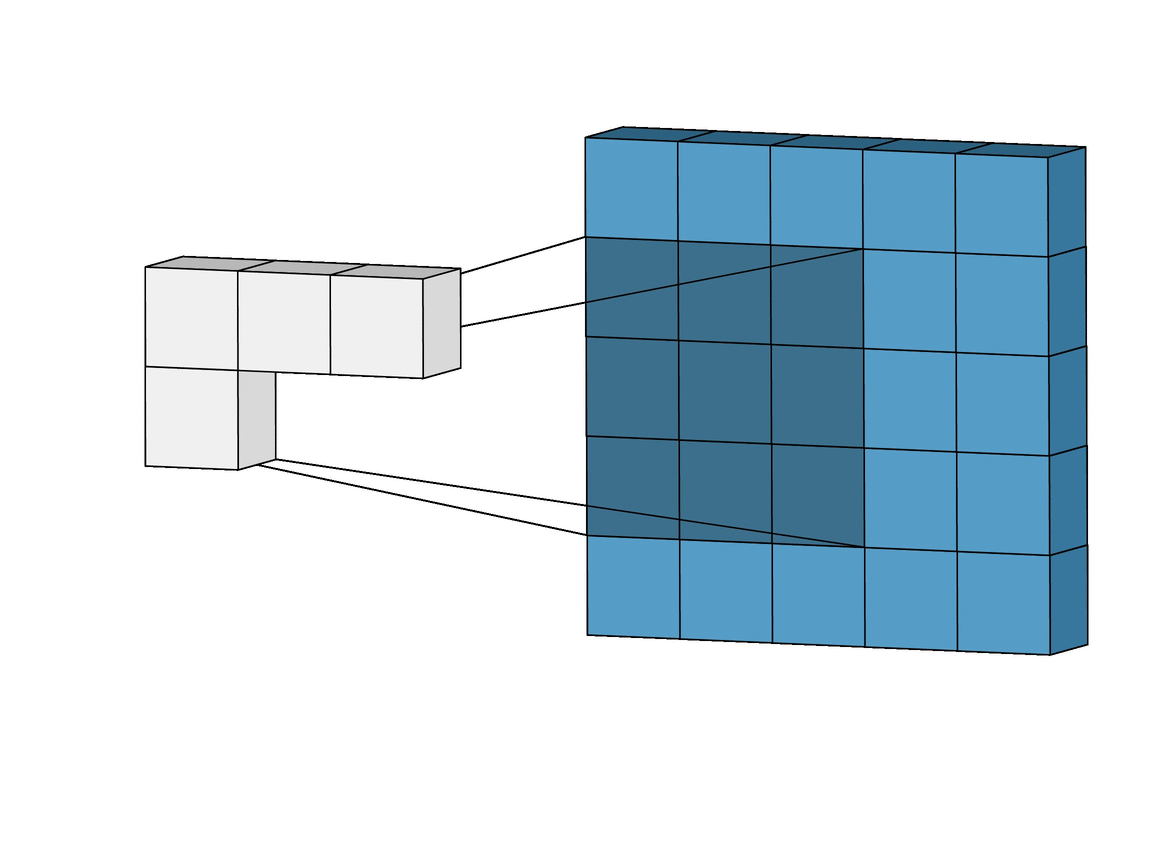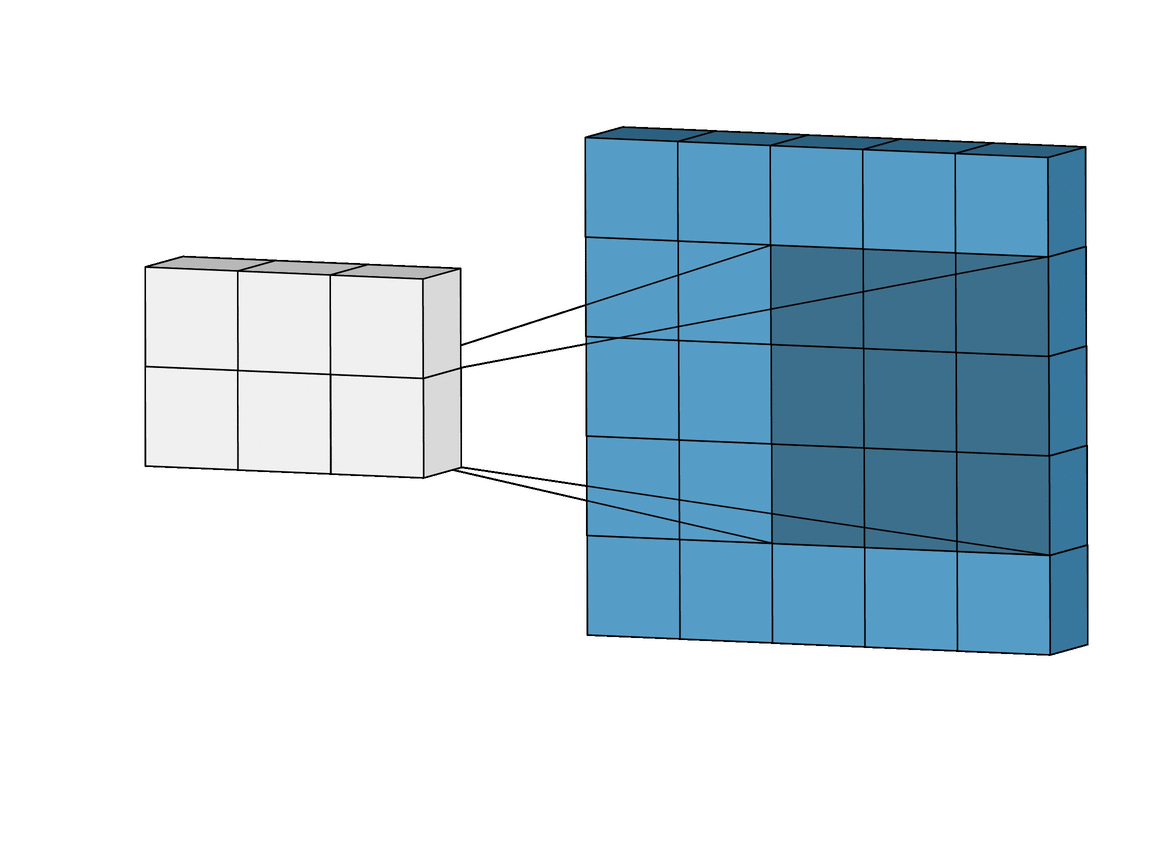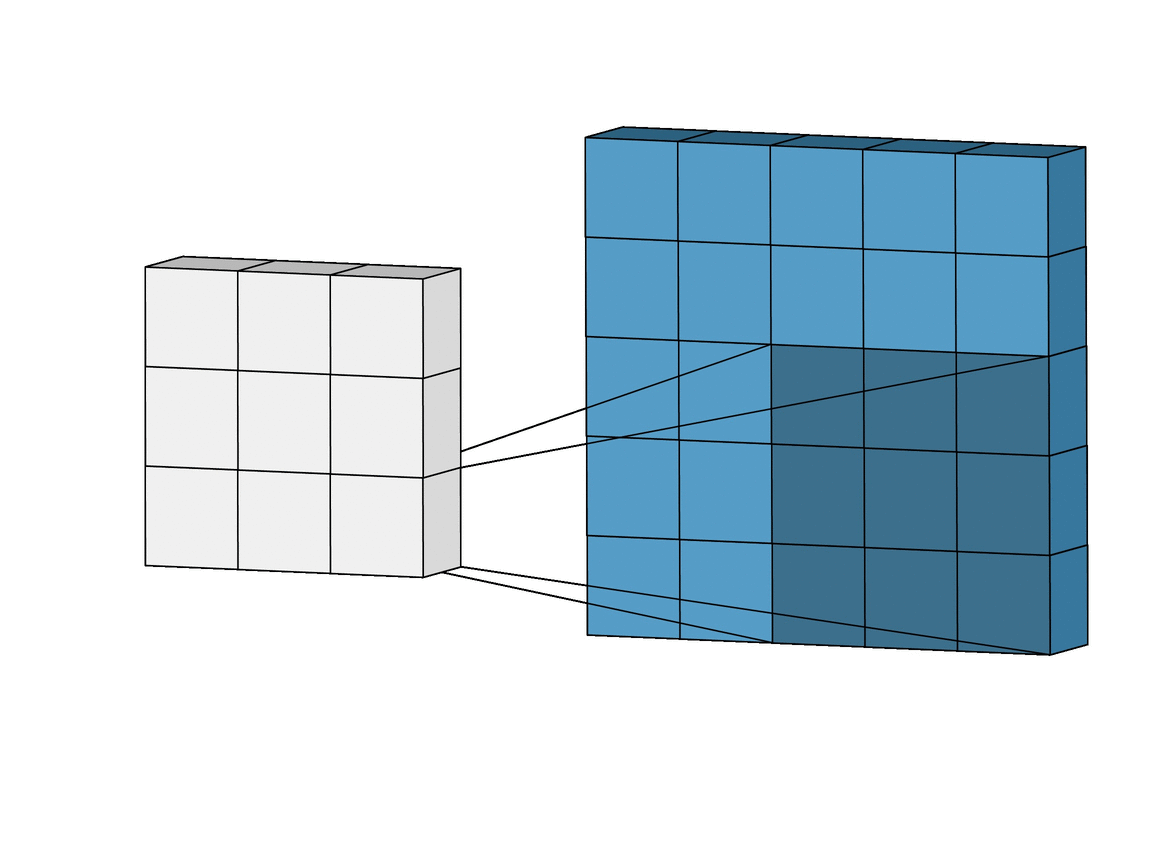
卷积的连接方式如上图所示，蓝色矩阵表示输入，绿色矩阵表示输出，每个绿色块与 9 个蓝色块连接。

把卷积核用矩阵表示如下：

为了便于理解，我们把卷积写成矩阵乘法的形式。先把输入矩阵 $\mathbf{x}$ 从一个 $4 \times 4$ 的矩阵以行优先方式拉伸成一个长度为 16 的向量，把输出矩阵 $\mathbf{y}$ 从一个 $2\times2$ 的矩阵以同样的方式拉伸成长度为 4 的向量，然后把 $\mathbf{w}$ 表示成 $4\times16$ 的稀疏矩阵 $\mathbf{C}$：

则卷积的过程可以描述为：

转置卷积

Transposed Convolution

转置卷积就是已经有了一个 $2\times2$ 的矩阵 $\mathbf{y}$，想要获得一个 $4 \times 4$ 的矩阵 $\mathbf{x}$。则根据矩阵相乘的原理，我们可以找一个 $16\times4$ 的稀疏矩阵 $\mathbf{C}$，然后利用公式 $\mathbf{C} \cdot \mathbf{y} = \mathbf{x}$ 得到矩阵 $\mathbf{x}$。这个稀疏矩阵与之前在卷积过程中用到的稀疏矩阵在尺寸上恰好是转置关系。

需要注意的是，转置卷积的卷积核与卷积的卷积核不一定相关，具体需要根据应用场景来确定：

  1. 在特征可视化、训练阶段的反向传播中，通常会需要使用转置卷积来进行特征重构。但是在实际的网络中，转置卷积并不是作为一个真正的 layer 存在于网络中。这是因为转置卷积（反向传播）的过程可以看作是卷积（正向传播）的逆过程，因此在这个过程中并不需要额外的参数或者计算。所以在这种情况下，可以使用转置卷积核（将卷积核中心对称后得到一个新的卷积核）来实现转置卷积的计算，而无需将其作为一个真正的 layer 加入到网络中。
  2. 在图像分割、生成模型、decoder 中使用的转置卷积，是网络中真实的 layer，其卷积核经初始化后需要通过学习获得（所以卷积核也就无所谓是不是通过卷积操作的卷积核的中心对称后得到的了）。

相关计算

卷积

卷积的输出尺寸计算公式如下：

输入尺寸：

输出尺寸：

则：

如果不能整除，统一向下取整。

假设输入特征图大小为 (3, 64, 64)，卷积核大小为 4，步长为 2，填充为 1，则输出特征图大小为 (3, 32, 32)。

为了简化，我们可以只考虑输入和输出都是长宽相等的矩阵。

设卷积过程的输入尺寸为 $i$，输出尺寸为 $o$，padding 为 $p$，卷积核大小为 $k$，步长为 $s$，则：

在深度学习框架中，根据 $p$ 的不同，有三种不同的卷积模式，分别是 SAME，VALID 和 FULL。这三种模式会导致输出的尺寸不同。

FULL

VALID

SAME

  1. FULL 模式：卷积核从与输入有一个点的相交的地方就开始卷积，$p$ 值最大，为 $k-1$。该模式卷积后输出的尺寸最大。
  2. VALID 模式：在整个卷积核与输入重叠的地方开始卷积操作，不需要 padding，即 $p=0$。该模式卷积后输出的尺寸最小。
  3. SAME 模式：卷积后输出的尺寸与输入尺寸保持一致（由于 $p$ 的最大值为 $k-1$，简单计算可以得到此时要么 $s=1$，要么 $i\le2$，我们只考虑 $s=1$ 的情况）。此时把卷积核的中心与输入的第一个点进行对齐就可以确定卷积核起始位置，然后补齐对应的 padding 即可，也就是说此时 $p=\frac{k-1}{2}$。如果卷积核的边长是偶数，可以在 padding 的时候只补充一条边（不对称 padding）。

总而言之，卷积与转置卷积互为逆过程，它们使用的卷积核可以通过中心对称进行转换。

转置卷积

转置卷积输出特征图尺寸的计算公式如下：

输入尺寸：

输出尺寸：

则：

例如，假设输入特征图大小为 (3, 32, 32)，卷积核大小为 4，步长为 2，填充为 1，则输出特征图大小为 (3, 64, 64)。

为了简化，我们可以只考虑输入和输出都是长宽相等的矩阵，且忽略 。

设转置卷积的输入尺寸为 $i’$，输出尺寸为 $o’$，padding 为 $p’$，卷积核大小为 $k’$，步长为 $s’$，则：

卷积与转置卷积对比

为了把卷积与转置卷积进行比较，我们考虑卷积过程的输入尺寸为 $i$，输出尺寸为 $o$，padding 为 $p$，卷积核大小为 $k$，步长为 $s$，则转置卷积的输入尺寸为卷积的输出尺寸 $o$，输出尺寸为卷积的输入尺寸 $i$。则根据公式 $(1)$ 可以得到：

因为转置卷积也是卷积，则可以把上面的式子整理如下：

我们令：

则有：

其中每个参数我们可以按照下面的方法去理解：

  • $i’= o+(o-1)(s-1)$：卷积的输出为 $o \times o$ 的矩阵，每行每列都是 $o$ 个元素，有 $o-1$ 个间隔，转置卷积时在每个间隔处插入 $s-1$ 个 $0$ 值，就可以构成转置卷积的输入。

  • $p’ = k-p-1$：在上一步得到的输入的基础上再进行 padding，考虑卷积的三种情况：

    • VALID：$p=0$，转置卷积则需要 $p’=k-1$，对应 FULL padding
    • SAME：$p=\frac{k-1}{2}$，只考虑 k 为奇数的情况，则 $p’=\frac{k-1}{2}$，对应 SAME padding
    • FULL：$p=k-1$，则 $p’=0$，对应 VALID padding

    可见卷积和转置卷积的 padding 也具有某种对称性，满足 $p’+p=k-1$。

  • $k’=k$：转置卷积与卷积的卷积核大小相同。

  • $s’=1$：转置卷积的步长均为 $1$。

FULL_Transposed

VALID_Transposed

SAME_Transposed

以上我们只考虑了公式 $(1)$ 可以被整除的情况，但如果 $\frac{i + 2p - k}{s}$ 不能被整除，则按照上面的方法计算得到的 $o’=\frac{i’ + 2p’ - k’}{s’} + 1$ 将小于 $i$。在卷积过程中就被丢弃的部分的大小为

因此我们可以得到：

为了让 $o’=i$，我们可以令：

只需要在 padding 后，在下边和右边再扩展 $a$ 行和 $a$ 列 $0$ 值，然后进行卷积即可。

注意，因为 $s’=1$，我们可以把 $a$ 放在分母位置上，也可以把它放在外面，之所以我们选择把她放在分母上，是因为在卷积的过程中，输入的下边和右边的 $a$ 行或 $a$ 列中的元素可能参与了运算，即与卷积的输出存在连接，所以在转置卷积的过程中，为了保持相同的连接，最后扩展的 $a$ 行和 $a$ 列也要参与卷积，所以放在分母上。

应用

卷积

卷积神经网络（CNN）作为特征提取器，通过一系列的卷积和池化操作，可以将输入图像转换为一组特征图或特征向量，这些特征图或者特征向量可以用于物体的分类和位置回归、人脸的对比和识别、语音的识别与分析等任务。

转置卷积

  1. GANs 中的图像生成

    生成对抗网络（GANs）是一种深度学习模型，常用于生成逼真的图像。GANs 由两个神经网络组成：生成器网络和判别器网络。生成器网络通过输入一个噪声向量，输出一张逼真的图像；判别器网络则通过输入一张图像，输出这张图像是否是真实的。

    转置卷积在 GANs 中被广泛应用于生成器网络中。生成器网络通常由一些转置卷积层（包括 ConvTranspose2d）和一些归一化层（如批归一化）组成。通过不断调整生成器网络的参数，可以使其输出的图像越来越逼真。

  2. 图像分割任务

    图像分割是计算机视觉中的一个重要任务，其目标是将一张图像分成多个互不重叠的区域，每个区域对应一个物体或者背景。转置卷积在图像分割任务中常用于上采样，将低分辨率的特征图转换为与输入图像相同大小的特征图，从而得到更加精细的分割结果。

    在图像分割任务中，通常使用编码器-解码器结构的网络。编码器网络通过一系列的卷积和池化操作，将输入图像转换为一组特征图；解码器网络则通过一些转置卷积和插值操作，将这些特征图逐步上采样并融合，最终得到与输入图像相同大小的分割结果。

卷积和转置卷积的区别

转置卷积通常用于生成模型中，如图像生成、超分辨率和图像分割等任务，而卷积则主要用于分类、检测等任务中。

在实际应用中，转置卷积和卷积操作可以相互结合，构建更加复杂的神经网络模型。

PyTorch 中的实现

ConvTranspose2d

ConvTranspose2d 是 PyTorch 深度学习框架中的一个二维转置卷积层。它是卷积神经网络中常用的一种层，可以将低维特征图转换为高维特征图。

ConvTranspose2d 层的输入和输出都是四维张量，分别代表样本数、通道数、高度和宽度。

ConvTranspose2d 层的基本参数如下：

1
class torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True)
in_channels(int) 输入通道数
out_channels(int) 输出通道数
kerner_size(int or tuple) 卷积核大小
stride(int or tuple,optional) 卷积步长，默认为 1
padding(int or tuple, optional) 为输入的每一条边补充 0 的层数，默认为 0
output_padding(int or tuple, optional) 为输出的每一条边补充 0 的层数，默认为 0
dilation(int or tuple, optional) 卷积核元素之间的间距，默认为 1
groups(int, optional) 从输入通道到输出通道的阻塞连接数
bias(bool, optional) 如果 bias=True，添加偏置，默认为 True

Conv2d

Conv2d 是 PyTorch 深度学习框架中的一个二维卷积层。它是卷积神经网络中最基本的一种层，可以从输入特征图中提取出不同的特征信息。

Conv2d 层的输入和输出都是四维张量，分别代表样本数、通道数、高度和宽度。

Conv2d 层的基本参数如下：

1
class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')
in_channels(int) 输入通道数
out_channels(int) 输出通道数
kerner_size(int or tuple) 卷积核大小
stride(int or tuple,optional) 卷积步长，默认为 1
padding(int or tuple, optional) 为输入的每一条边补充 0 的层数，默认为 0
dilation(int or tuple, optional) 卷积核元素之间的间距，默认为 1
groups(int, optional) 从输入通道到输出通道的阻塞连接数
bias(bool, optional) 如果 bias=True，添加偏置，默认为 True
padding_mode(string, optional) padding 的模式，默认为 ‘zeros’，也可以是 ‘reflect’、’replicate’ 或 ‘circular’

代码实现

ConvTranspose2d

ConvTranspose2d 层的定义如下：

1
2
3
4
5
6
7
8
9
import torch.nn as nn

conv_transpose = nn.ConvTranspose2d(
    in_channels=3,
    out_channels=3,
    kernel_size=4,
    stride=2,
    padding=1
)

通过调用 ConvTranspose2d 的 forward 方法，可以将输入特征图进行上采样：

1
2
3
4
5
import torch

x = torch.randn(1, 3, 32, 32)
y = conv_transpose(x)
print(y.size())  # 输出 (1, 3, 64, 64)

在上采样的过程中，ConvTranspose2d 层可以学习特征图之间的权重关系，从而生成更加真实、清晰的高分辨率图像。

Conv2d

Conv2d 层的定义如下：

1
2
3
4
5
6
7
8
9
import torch.nn as nn

conv = nn.Conv2d(
    in_channels=3,
    out_channels=3,
    kernel_size=4,
    stride=2,
    padding=1
)

通过调用 Conv2d 的 forward 方法，可以将输入特征图进行卷积操作：

1
2
3
4
5
import torch

x = torch.randn(1, 3, 64, 64)
y = conv(x)
print(y.size())  # 输出 (1, 3, 32, 32)

在卷积的过程中，Conv2d 层通过不断滑动卷积核对输入特征图进行扫描，并在每个位置进行点乘和加和运算，得到相应的输出特征图。Conv2d 层可以学习卷积核的权重，从而提取输入特征图中的高层次特征，用于后续的分类、检测、分割等任务。

Conclusion

ConvTranspose2d 作为一种上采样操作，可以将低分辨率的输入图像变换成高分辨率的输出图像。它的优点在于可以直接从原始数据中生成高分辨率图像，并且不会出现模糊的情况。同时，ConvTranspose2d 也具有可逆性，因此可以应用于图像的压缩和解压缩等任务。但是，ConvTranspose2d 也存在一些缺点，例如生成的图像可能存在伪影、失真等问题。

References

  1. ConvTranspose2d（逆卷积）的原理和计算
  2. 一文搞懂 deconvolution、transposed convolution、sub-pixel or fractional convolution
  3. 卷积 Convolution 原理及可视化
  4. Convolution arithmetic
  5. ConvTranspose2d — PyTorch 2.0 documentation
  6. Conv2d — PyTorch 2.0 documentation